振動 方程式
結構運動方程式 自由振動 () 0 振動頻率 () 0 () 0 2 0 xt xt xt m k xt mxt kxt Z F(t) 0 m k Z 0 若質量m 相同, 則勁度k 越大,頻率f 越高,週期T 越短。 若勁度k 相同, 則質量m 越大,頻率f 越低,週期T 越長。 Second order homogeneous ordinary differential equation with constant coefficients.

振動 方程式. XMind is the most professional and popular mind mapping tool Millions of people use XMind to clarify thinking, manage complex information, brainstorming, get work organized, remote and work from home WFH. 假設振子不再受到其他外力的作用,於是可利用牛頓第二定律寫出系統的振動方程式: ∑ F = m a = m x ¨ = m d 2 x d t 2 {\displaystyle \sum F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}}. 3/10 02 弦の振動方程式 安江正樹@東海大学理学部物理学科 2, tan xxdx uxt x (211) このtan 1とtan 2を利用して三角関数cos 1, sin 1とcos 2, sin 2を表すことができればよい。 そのため、ごくわずかに振動している場合(微小振動)を考える。.
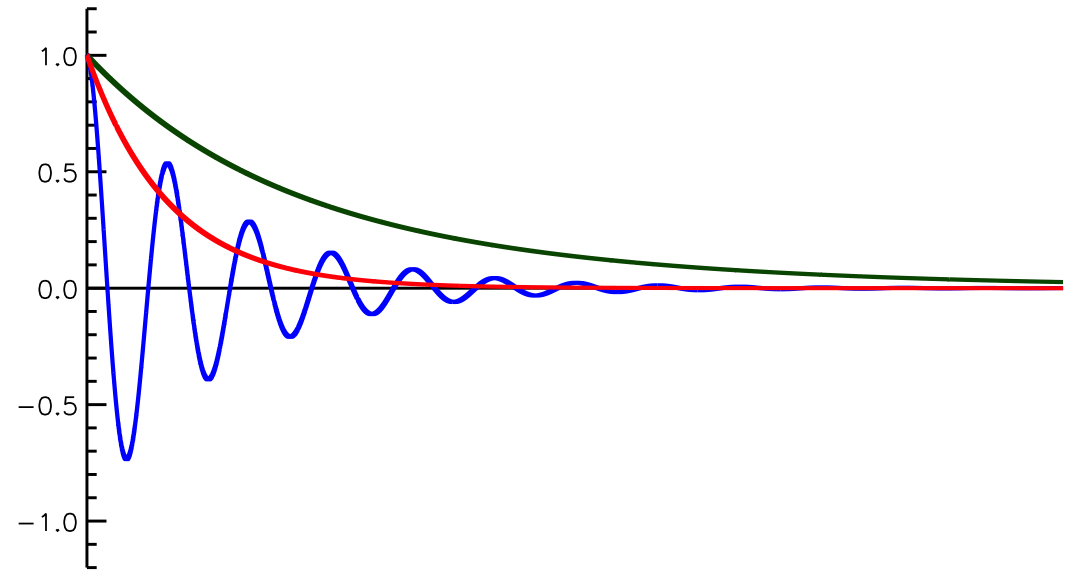
該振動解表徵的是一種振幅按指數規律衰減的簡諧振動,稱為衰減振動(見上圖中 的位移時間曲線所示)。 對於臨界阻尼體系,運動方程式的解具有形式 ;. 方程式 x(t)=Acos(ωt φ) 代入成立 A 與φ 為任意常數 理論上可以用數學轉換 也可以用 x(t)=Bsin(ωt ψ) B 與ψ 為任意常數 x(t) A sin(ωt)()A cos ωt A 1 與A 2 為任意常數 = 1 2 這些都是簡諧運動方程式的解 微分方程式的求解方式:工程數學或應用數學. 調和振動子の量子力学的取扱い 一般の束縛状態と調和振動子 1次元の井戸型ポテンシャルの中での束縛状態は,そのシュレディンガー方程式を近似 なしで容易に解くことができ,かつエネルギー固有値が離散的になるといった量子論特有.
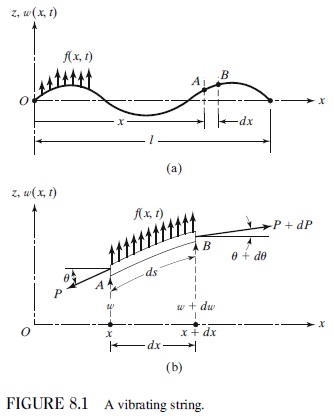
§5 振動(その2) 1 振動の減衰 前回の授業では、摩擦のない理想的な場合の振動を考察した。その振動は、一定の周期と振幅で、 無限に続くと予言される。しかし、現実の系では必ず摩擦力が働き、振動の減衰が起こることを我々 は経験から知っている。. ω = 2 π ⋅ f {\displaystyle \omega =2\pi \cdot f} , 為振動的 角頻率 。 通過 角頻率 簡寫為: y ( t ) = y 0 ⋅ sin ( ω t φ 0 ) {\displaystyle y (t)=y_ {0}\cdot \sin (\omega \,t\varphi _ {0})\,} 對時間求導得到: v ( t ) = ω ⋅ y 0 ⋅ cos ( ω t φ 0 ) {\displaystyle v (t)=\omega \cdot y_ {0}\cdot \cos (\omega \,t\varphi _ {0})\,} 其中. 一維波傳方程式 若u x,t 表繩上質點因波動所引致之垂直位移量,則根據牛頓第二運動定律可建 立出問題之控制方程式(Governing Equation): 2 2 2 2 2 1 t u x c u 其中係數c稱為波傳速度(Wave Velocity) 。上式常稱之為一維波傳方程式。 證明: 如圖1 所示之弦索振動:.
3 二階線性微分方程式(第101 頁) 這一章要討論某幾類特別的二階線性微分方程。 在數學上, 討論它們的原因在於這類的微 分方程可以把解確實地寫出來, 並且當中有一些數學理論值得探討, 特別是解空間有線性 代數的結構。 在物理上, 二階線性微分方程自微積分發展的過程中就已被用來了解許多自. 単振動の一般解 単振動の一般解が, x =C1cosω0t C2sinω0t (72) なる形で,2 つの特解の一次結合(重ね合わせ)として表されることが,自然に理解できない. 回答 特解がcosω0t であることがわかっている時,u をt の未知の関数として,単振動の解をucosω0t と おくと,u の一般解が,. 振動沿著軸線方向傳播,在桿件的振動中可分為三類,即縱向振動、 橫向振動和扭轉振動。 (1) 縱向振動:因為振動沿桿件軸向傳播,因此作縱向振動時,桿件 上各點振動方向與軸平行。 (2) 橫向振動:作橫向振動時,桿件上各質點振動方向與軸垂直。.
単振動 : 運動方程式 (equation of motion) 原点 O を中心として, x 軸に沿って角振動数 ω で単振動する質量 m の質点の位置 x と加速度 a の関係は a = − ω 2 x である ので,単振動する質点の運動方程式は m a = − m ω 2 x = − c x , c = m ω 2 (1) と表せる.よって, x 軸上を単振動する質点には. 電磁振動方程式 單色平面波和球面波都是波動方程式的特解 在空間固定點觀察,電磁振動方程式可用餘弦函數表示: 亦可用複數表示: Re 0 0 0 ei t H E H E 0 0 0 cos t H E H E 0 0 0. 駐波(英語: standing wave 或 stationary wave )為兩個波長、週期、頻率和波速皆相同的正弦波相向行進干涉而成的合成波。 與行波不同,駐波的波形無法前進,因此無法傳播能量,故名之。 駐波通過時,每一個質點皆作簡諧運動。 各質點振盪的幅度不相等,振幅為零的點稱為節點或波節(英語: Node.
ねじり振動(241) 図113 ねじり振動系 θ N=kθ l r d k I Iθ&&=−kθ 角運動量の変化(慣性力)=外力モーメント (復原トルク) l Gd k 32 π 4 = 2 mr2 I = θ=Acosωnt Bsinωnt ばね質点系の運動方程式と同じ形 ωn = k / I Iθ&&kθ=0 横弾性率 G (鉄) ≒80GPa ⇒直径1mmの針金 を01%引張る. 振動問題 如圓膜的振動 u xx u tt /v 2 =0 如果把$\Psi(x,t)$拆成 $\psi(x)*\psi(t)$ 由於另一個當作常數 所以 只要對變數的部分進行兩次微分 ===> RHS=0 因此整理一下 可以把不要的term消去 (歸類在速度項)。 因為我大學不是物理系的 是上了物理所,. 電磁振動方程式 單色平面波和球面波都是波動方程式的特解 在空間固定點觀察,電磁振動方程式可用餘弦函數表示: 亦可用複數表示: Re 0 0 0 ei t H E H E 0 0 0 cos t H E H E 0 0 0.
一般解が上のように表されるとき、 「\(X=xx_0\)は、角振動数\(\omega\)、振動中心\(x_0\)の単振動をする」 といい、周期\(T\)は \T=\frac{2π}{\omega}=2π\sqrt{\frac{m}{k}}\ と表すことができます。この式から 質量\(m\)が大きいほど、周期\(T\)が大きくなる こともわかります。. 強制振動:外部が注入されているときに起こる振動 共振 外力の振動数が固有振動数に一致しているとき,振動が増幅されていく現象 高調波共振 外力の振動数が固有振動数の例えば約 になっているとき,その 倍の振動数の振動が大きく表れたりする現象. 振動問題 如圓膜的振動 u xx u tt /v 2 =0 如果把$\Psi(x,t)$拆成 $\psi(x)*\psi(t)$ 由於另一個當作常數 所以 只要對變數的部分進行兩次微分 ===> RHS=0 因此整理一下 可以把不要的term消去 (歸類在速度項)。 因為我大學不是物理系的 是上了物理所,.
第9回 弦の振動方程式の完全解 第9回は、弦の振動を表す偏微分方程式を解き、境界条件と初期条件を満足する完全解 を求める。解法は次の3ステップにまとめることができる。 (1)ステップ1:偏微分方程式を変数分離により常微分方程式に分解する。. 由於分析時須用到結構自身之自然頻率(natural freguency)和振態,因此應用此法分析時,須先解結構自然振動方程式。所謂自然振動(natural vibration)就是在無外力作用下,結構自身之自由振動(free vibration),其振動一般肇因於初位移(initial displacement)或初速度(initial. §5 振動(その2) 1 振動の減衰 前回の授業では、摩擦のない理想的な場合の振動を考察した。その振動は、一定の周期と振幅で、 無限に続くと予言される。しかし、現実の系では必ず摩擦力が働き、振動の減衰が起こることを我々 は経験から知っている。.
単振動 : 微分方程式の解法 (solution of differential equation) 角振動数 ω の単振動の従う微分方程式 d 2 x d t 2 ω 2 x = 0 (1) の一般解を求める: 解法1 解法2 (初期値問題は ⇒) 解法1. 波動方程式是雙曲形偏微分方程式的最典型代表,其最簡形式可表示為:關於位置x和時間t的純量函數u(代表各點偏離平衡位置的距離)滿足: ∂ 2 u ∂ t 2 = c 2 ∇ 2 u {\displaystyle {\partial ^{2}u \over \partial t^{2}}=c^{2}\nabla ^{2}u}. U(s) = mgl(1 cos ) (210) ただし、鉛直線からの棒の振れ角を とした。このとき、s = l 。 平衡点は = s = 0.
動力學方程式 對於一維的簡諧振動,其動力學方程式是二階微分方程式,可由牛頓第二運動定律得到 = = = ¨ 回復力又可表示為 = − 所以有 ¨ = 求解上述方程式,得到的的解含有正弦函數. 固有振動数 固有振動数とは、アンテナや回路、あるいは力学系において、共振周波数となる 振動数のこと 弾性定数k のバネに結ばれた質量m の質点の運動方程式と解は、 次のようになります。 k x m mx&&=−kx :ばねの自然長からの変位 k x m:質量 :ばね fn. 振動沿著軸線方向傳播,在桿件的振動中可分為三類,即縱向振動、 橫向振動和扭轉振動。 (1) 縱向振動:因為振動沿桿件軸向傳播,因此作縱向振動時,桿件 上各點振動方向與軸平行。 (2) 橫向振動:作橫向振動時,桿件上各質點振動方向與軸垂直。.
方程式 x(t)=Acos(ωt φ) 代入成立 A 與φ 為任意常數 理論上可以用數學轉換 也可以用 x(t)=Bsin(ωt ψ) B 與ψ 為任意常數 x(t) A sin(ωt)()A cos ωt A 1 與A 2 為任意常數 = 1 2 這些都是簡諧運動方程式的解 微分方程式的求解方式:工程數學或應用數學. 結構運動方程式 自由振動 () 0 振動頻率 () 0 () 0 2 0 xt xt xt m k xt mxt kxt Z F(t) 0 m k Z 0 若質量m 相同, 則勁度k 越大,頻率f 越高,週期T 越短。 若勁度k 相同, 則質量m 越大,頻率f 越低,週期T 越長。 Second order homogeneous ordinary differential equation with constant coefficients. で記述される運動を単振動あるいは調和振動という。 例:単振り子の場合 長さlの軽い棒につながった質量mの質点の力学的エネルギー E = 1 2 ms_2 U(s);.
エネルギーを元にして振動方程式を導く方法である。変分原理に基づく振動方程式は以下 のように表わせる。 22 11 0 tt tt ∫∫δδT V dt Wdt− = (25) ここで、t1とt2 は任意の時間を表わす。また、 T =全運動エネルギー. 其中a 和b 由初始條件所決定。該振動解表徵的是一種按指數規律衰減的非周期運動。 對於過阻尼體系,定義. 振動沿著軸線方向傳播,在桿件的振動中可分為三類,即縱向振動、 橫向振動和扭轉振動。 (1) 縱向振動:因為振動沿桿件軸向傳播,因此作縱向振動時,桿件 上各點振動方向與軸平行。 (2) 橫向振動:作橫向振動時,桿件上各質點振動方向與軸垂直。.
名詞解釋 彈性結構系統在平衡條件下,承受恒定態負載P(t)時,其運動方程式可表之如下: 上式之完全解(total solution)x T 包含有兩部分的解: x r =x c x p 式中,x c 是補解(complementary solution),滿足: 是暫態的(transient)振動現象,與結構自然振動有關,造成施力後開始振動時的暫態亂象,但很快會消失. 轉換,以至於整個結構系統作重複的運動,這種現象稱為自由振動(參考圖 11)。 初始位移(速度) 圖11 由初始位移(或速度)所引起的結構自由振動 112 自然頻率(natural frequency) 結構系統處於自由振動情況時,單位時間內的往復次數稱為該系統的自 然頻率。. 単振動で虚数解が出そうなときは、ほとんどの場合で加速度の符号忘れが原因 ですので、知っておくといいでしょう。復元力の符号を忘れる人はなぜか少ないんですよ。 単振動方程式 \(m\omega^2 x=Kx\).
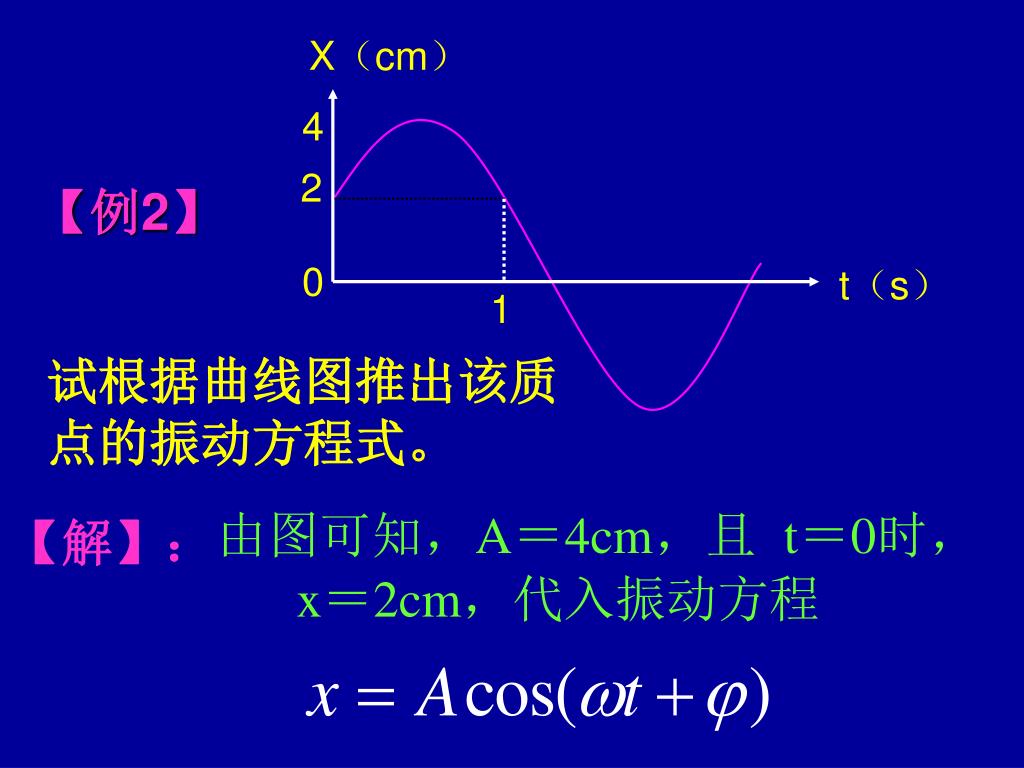
振動「週期」、「頻率」及「位移振幅」? 假設有一個質塊掛在 一個彈簧下面,如果此質 塊被壓縮或拉伸一段距 離,當釋放此壓縮或拉伸 力後,質塊將呈現上下來 回擺盪的現象,質塊上下 來回擺盪一次的時間,稱 為「週期」,單位以秒(sec) 表示;此週期的倒數即為 「頻率」,單位為赫茲 (Hz);而質塊上下來回擺 盪的距離,也就是質塊振 動的幅度,稱為「位移振 幅. 単振動 : 微分方程式の解法 (solution of differential equation) 角振動数 ω の単振動の従う微分方程式 d 2 x d t 2 ω 2 x = 0 (1) の一般解を求める: 解法1 解法2 (初期値問題は ⇒) 解法1.

解三角方程 如何解三角函数方程 三角函数方程解法 最简三角方程

梁のたわみの基礎方程式から 振動数方程式を導出する
微分方程式を用いた解法 減衰振動
振動 方程式 のギャラリー

第十章机械振动和电磁振荡 10 1 谐振动 10 2 阻尼振动 10 3 受迫振动共振 10 4 电磁振荡 Ppt Download

15年度秋学期 応用数学 解析 第11回 振動と微分方程式 15 12 3

動力學 許丁友 單元十七振動 6 黏滯阻尼自由振動 Youtube
二自由度系の振動 数学活用大事典

単振動の運動方程式 高校物理をあきらめる前に 高校物理をあきらめる前に

振動 維基百科 自由的百科全書

生物方程式 数学方程式 快乐方程式 电离方程式

梁のたわみの基礎方程式から 振動数方程式を導出する
Http Ocw Aca Ntu Edu Tw Ocw Files 105s106 105s106aa07l01 Pdf
Ppt 振動分析及實驗技術應用簡介powerpoint Presentation Free Download Id

Ppt 第3 章建筑抗震计算原理powerpoint Presentation Free Download Id
腾讯内容开放平台

弦側向振動方程式

振動方程式一般解

振動 維基百科 自由的百科全書
10 2 多自由度系の振動

工業力学入門講座 第27回 機械振動の基礎
世界第一簡單微分方程式 蝦皮購物
微分方程式で記述した物理現象の解析

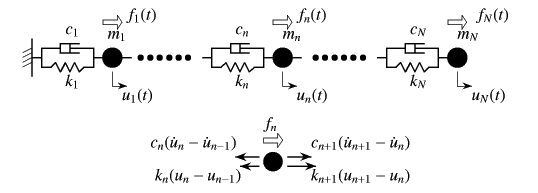
振动力学第四章多自由度系统的振动 Ppt 十八文库
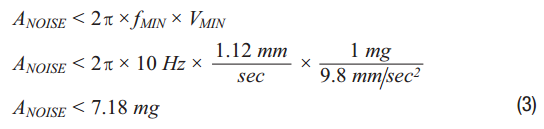
传感器的特性选择支招 这样轻松实现加速度和速度转换 科技频道 手机搜狐

粘性減衰力を考慮した1自由度振動系のモデルの一般解の応答
Http Ktlabo Cm Kyushu U Ac Jp J Common Img Shindou Rikigaku Pdf
Http Web Cjcu Edu Tw Ykchen Physics Handout Oscillatory motion Pdf
Ppt 第二章振动和波powerpoint Presentation Free Download Id

簡諧振動之解

1 非线性振动和线性振动的根本区别 4 2 一维非线性振动及其微分方程的近似解法方程 Ppt Download

6 1觀念04週期 頻率 波速與波動方程式 基礎物理 波 均一教育平台
微奈米技術實驗室
Ocw Chu Edu Tw Mod Resource View Php Id 811

Kevin Yu S Blog 振動學ch0503 無阻尼系統自由振動

D 2 Dt 2 2p Dx Dt W 2x 0怎么解 物理在学阻尼震动 雨露学习互助

非線性振動 單擺運動方程式之數值分析與研究 臺灣網路科教館

船用电机结构和振动方程式是什么 上海承务实业
Kevin Yu S Blog 振動學ch0802 弦或纜繩的垂直振動

単振動と微分方程式 1011 Gif

第十四章结构动力学 14 1 概述 14 2 结构振动的自由度 14 3 单自由度结构的自由振动 Ppt Download

振动力学基础与matlab应用 日文好书推荐 振动与噪声控制技术for机械设计者 Weixin 的博客 Csdn博客
Http Netedu Xauat Edu Cn Jpkc Netclass Jpkc Lx Jxzy Wljc 17 Pdf

國家地震工程研究中心national Center For Research On Earthquake Engineering 1 國立台灣海洋大學河海工程學系耐震設計 一 單自由度無阻尼結構之強迫振動鍾立來 Ppt Download
振動噪音產學技術聯盟 振動噪音科普專欄 質塊彈簧系統 自然頻率 Natural Frequency

波方程式世界 Hoi S Blog
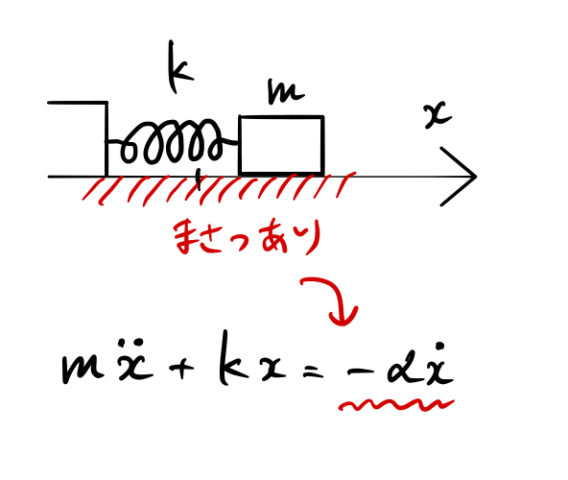
減衰振動 臨界振動 過減衰の運動方程式と一般解 そのイメージ ばたぱら

15年度秋学期 応用数学 解析 第11回 振動と微分方程式 15 12 3

微分方程式を用いた解法 減衰振動

単振動の運動方程式と一般解 高校物理の備忘録

振动力学下载 Ppt模板 爱问共享资料
/2002/2/%E9%9B%99%E6%93%BAbeating_p3.jpg)
海洋大學 力學聲響振動研究室

歐拉 伯努利 達朗貝爾關於弦振動問題的論戰 催生了傅立葉級數 每日頭條

単振動の微分方程式の解き方と一般解 理系ラボ

第十四章结构动力学 14 1 概述 14 2 结构振动的自由度 14 3 单自由度结构的自由振动 Ppt Download
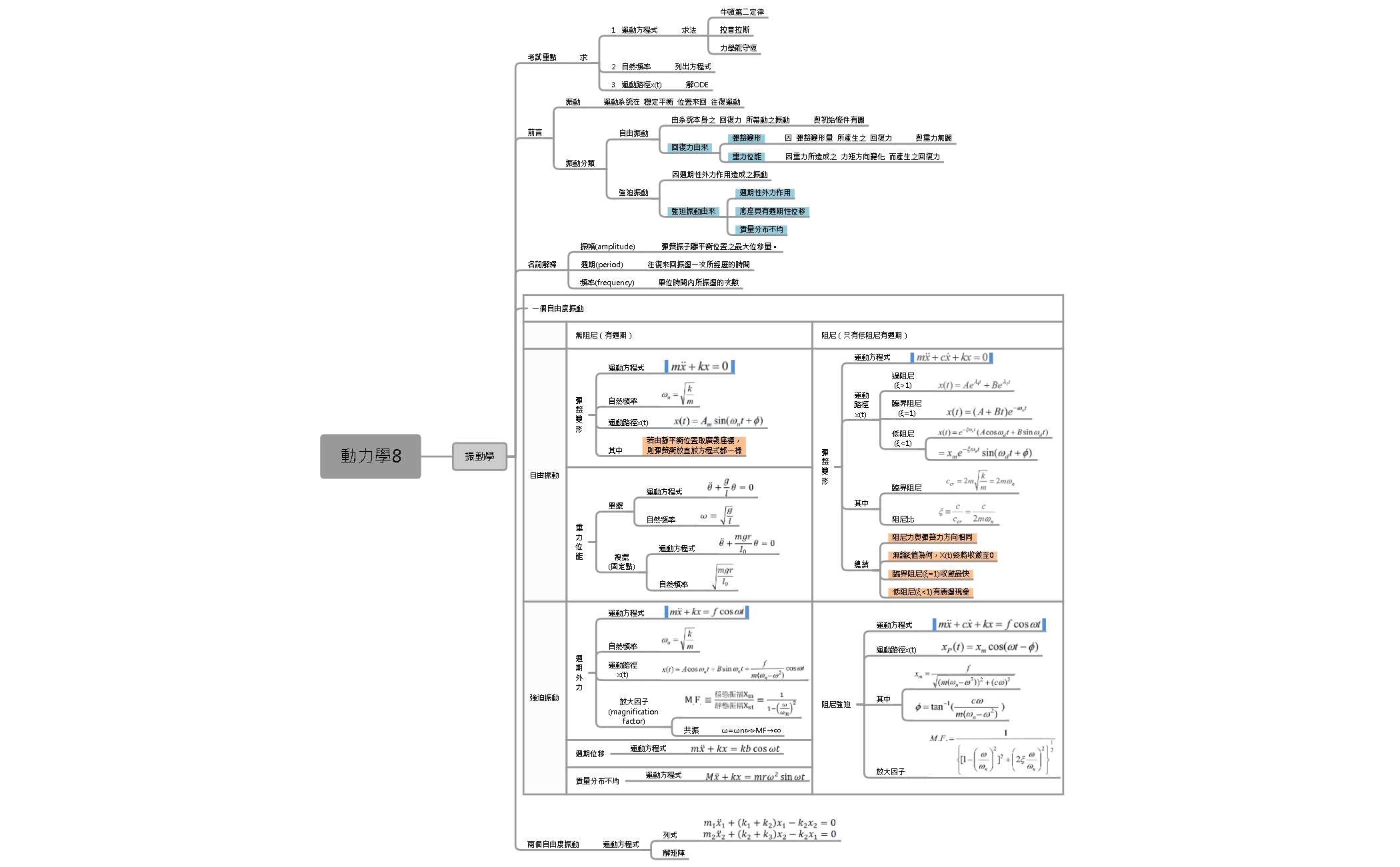
動力學8 振動學 Xmind Mind Mapping Software

國家地震工程研究中心national Center For Research On Earthquake Engineering 1 國立台灣海洋大學河海工程學系耐震設計 一 結構之基本振動週期鍾立來 Ppt Download

國家地震工程研究中心national Center For Research On Earthquake Engineering 1 國立台灣海洋大學河海工程學系耐震設計 一 單自由度無阻尼結構之強迫振動鍾立來 Ppt Download
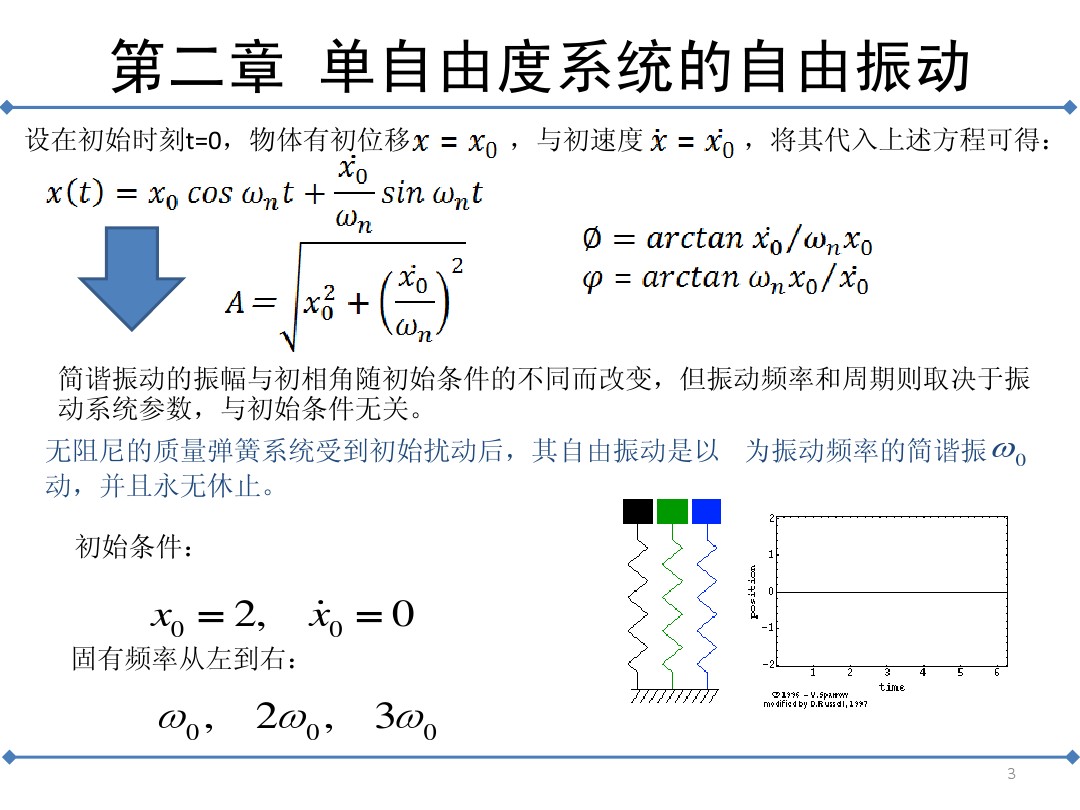
第二章单自由度系统的自由振动 图文 百度文库

振动力学第四章多自由度系统的振动 Ppt 十八文库

博客來 振動學 第二版
調和振動子 自由振動 強制振動 減衰振動 強制減衰振動

1 非线性振动和线性振动的根本区别 4 2 一维非线性振动及其微分方程的近似解法方程 Ppt Download

微分方程式6 斉次線形微分方程式その3 減衰振動 Youtube
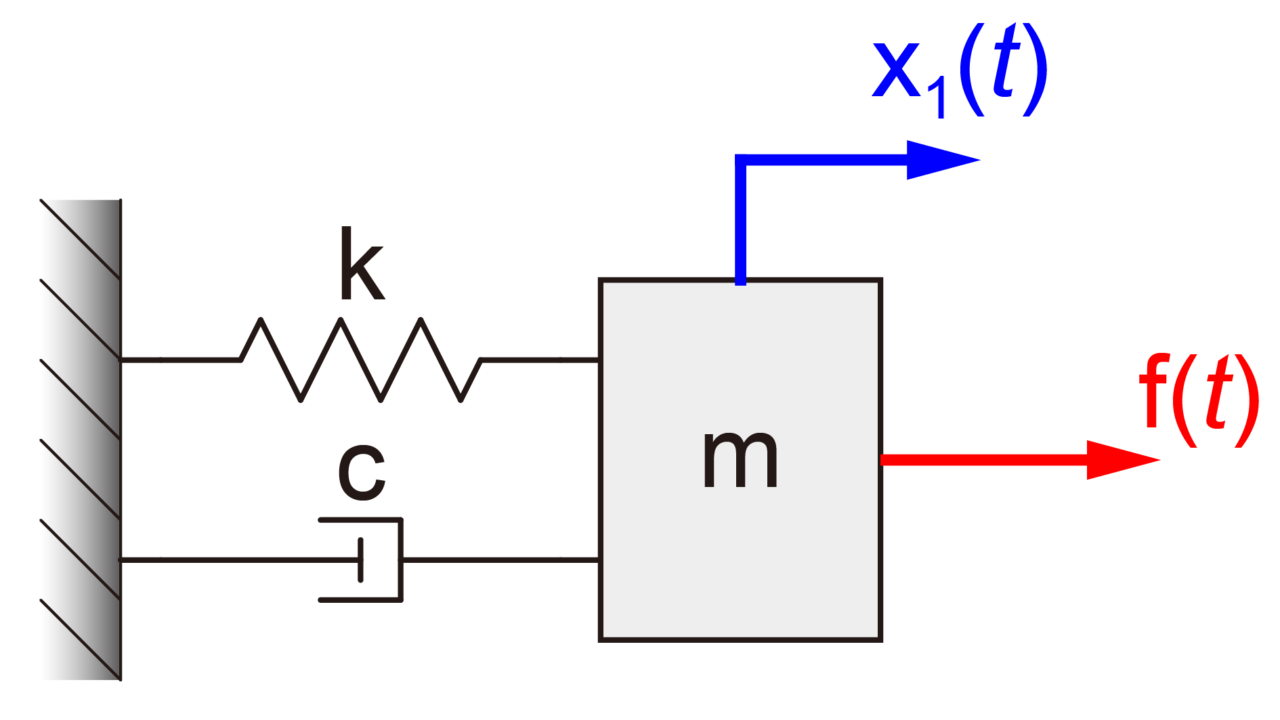
1自由度振動系の運動をマスターする 制御工学の基礎 Tajima Robotics

波動方程 波動方程 Wave Equation 是一種重要的偏微分方程 百科知識中文網
Http Web Cjcu Edu Tw Ykchen Physics Handout Oscillatory motion Pdf
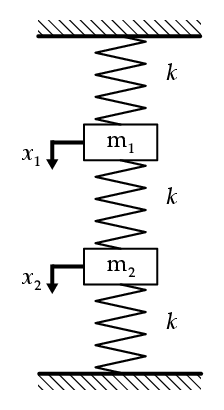
二自由度系の振動 数学活用大事典
Ocw Chu Edu Tw Pluginfile Php 6 Mod Resource Content 38 Summary 284 Pdf

振動の話

Ctimes Mems振動監測 從加速度到速率 Mems 微機電 速度計 振動感測器 振動監測 Cbm系統 Adi 美商亞德諾 亞德諾半導體

振動方程式一般解

連成振動 Miya Lab

振动与波动的原理图 第1页 一起扣扣网
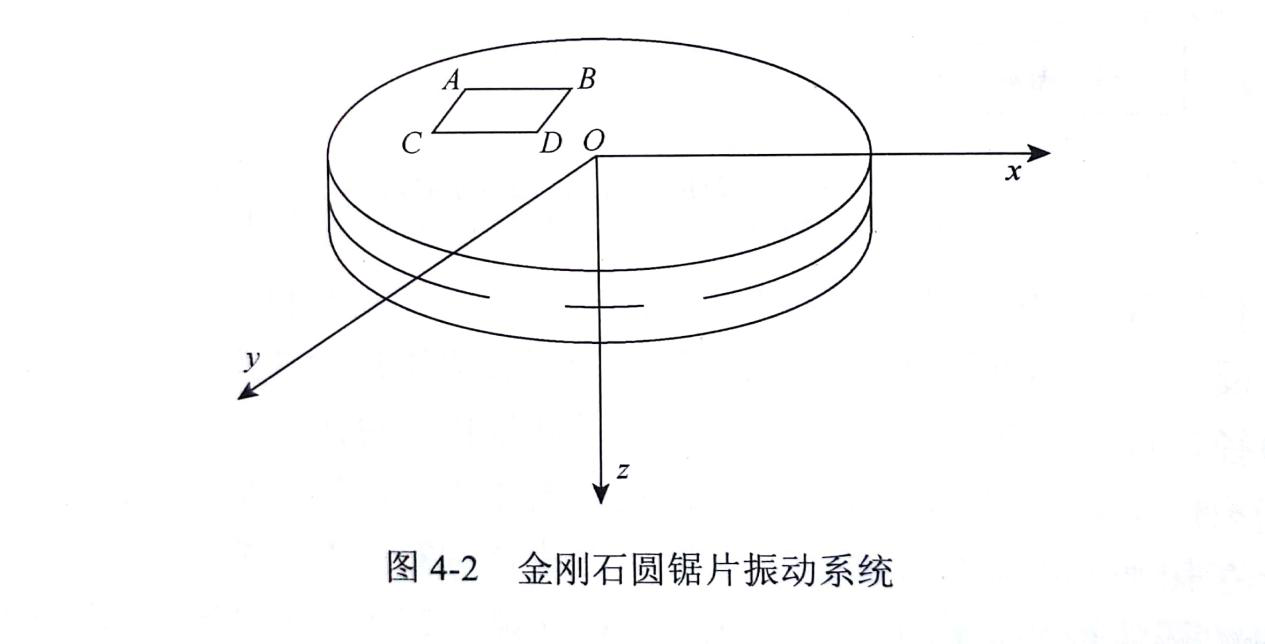
探究金刚石切割片的横向振动方程式的建立 金刚石切割片 切割片 昌利金刚石锯片
简谐振动运动方程的推导 知乎

单自由度振动方程与matlab Simulink求解 简书
Www Wun Ching Com Tw Img Books Files e2 Trial Pdf

简谐振动的运动学方程是怎么来的 知乎

単振動 慣性モーメント 運動方程式 物理に関する質問 勉強質問サイト
/2002/2/0112000.gif)
海洋大學 力學聲響振動研究室

振動學修訂版 露天拍賣

歐拉 伯努利 達朗貝爾關於弦振動問題的論戰 催生了傅立葉級數 每日頭條
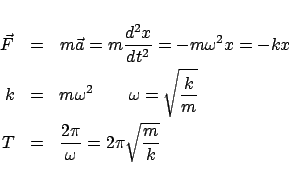
単振動の運動方程式

振動噪音產學技術聯盟 八月
調和振動子 自由振動 強制振動 減衰振動 強制減衰振動
Http Web Cjcu Edu Tw Ykchen Physics Handout Oscillatory motion Pdf

振動方程式一般解

空気抵抗や摩擦のある振り子の単振動
Http Mems Mt Ntnu Edu Tw Document Class 101 E4 B8 8a E5 Ad B8 E6 9c 9f Vibration Chapter 00 E8 B2 E7 A8 8b E5 E7 B6 B1 E8 87 E8 B2 E7 A8 8b E6 A8 E6 84 8f E4 Ba 8b E9 A0 85 Pdf

莱仕达方程式pxn V36 有线振动方向盘 报价 参数 图片 论坛 莱仕达方程式pxn V36 有线振动方向盘方向盘报价 Zol中关村在线

弦側向振動方程式
Http Ocw Aca Ntu Edu Tw Ocw Files 105s106 105s106aa07l01 Pdf
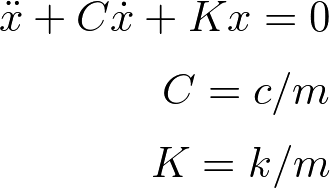
固有振動数と減衰比の計算
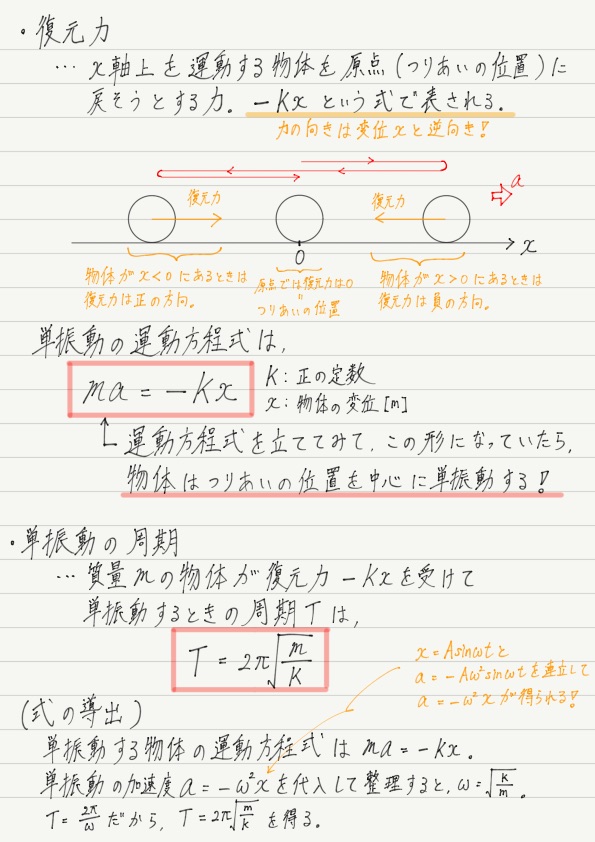
単振動の運動方程式 高校物理をあきらめる前に 高校物理をあきらめる前に
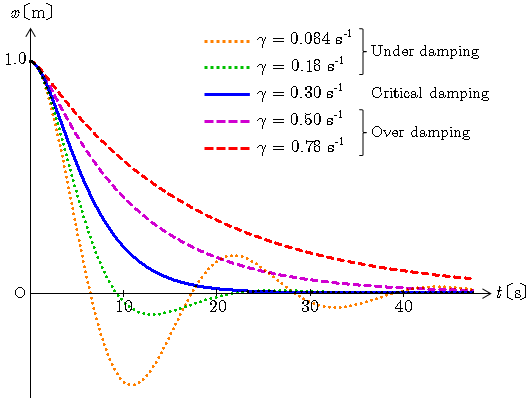
減衰振動 運動方程式

Ctimes Mems振動監測 從加速度到速率 Mems 微機電 速度計 振動感測器 振動監測 Cbm系統 Adi 美商亞德諾 亞德諾半導體
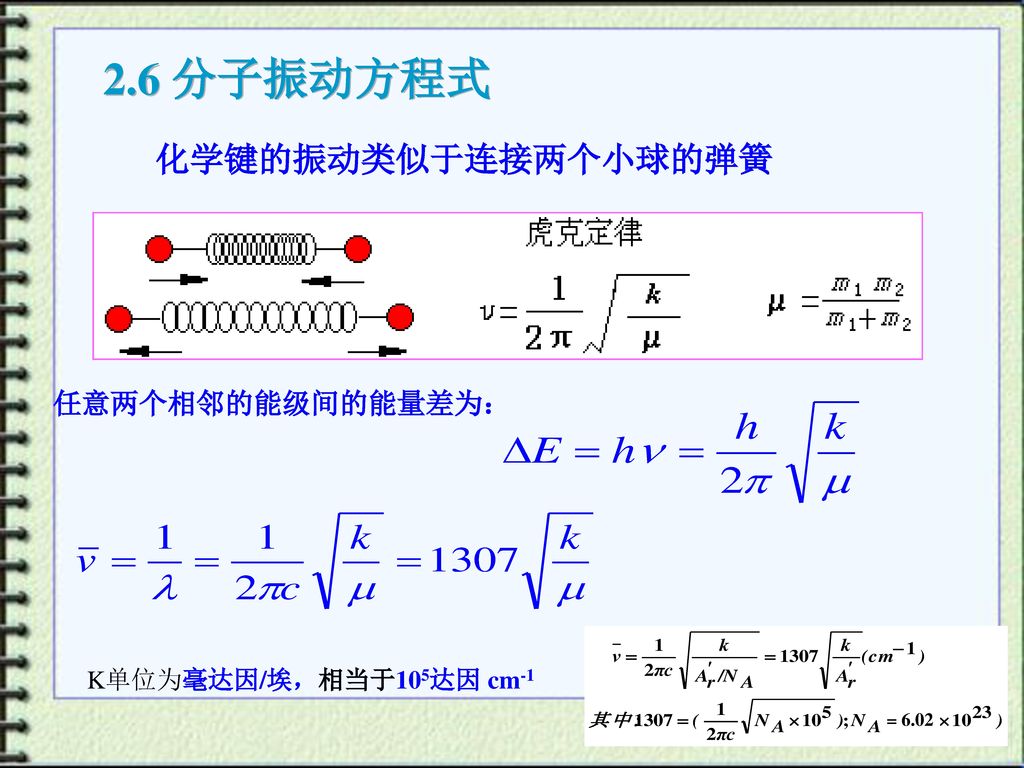
第一节红外光谱分析基本原理第二节仪器简介与实验技术第三节影响振动频率的因素第四节红外特征吸收与光谱解析第五节拉曼光谱法

歐拉 伯努利 達朗貝爾關於弦振動問題的論戰 催生了傅立葉級數 每日頭條

動力學 許丁友 單元十七振動 1 緒論 無阻尼自由振動 1 Youtube

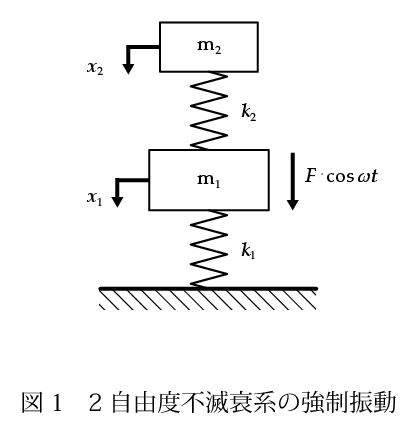
1 As Shown In Figure 1 A Double Free Vibration Chegg Com




